Friday, September 29, 2017
Gamecube controller to USB adapter
Loss of vice and growth of virtue
Here is a pattern in the moral life. People have a conversion experience and puts away “the gross sins of the flesh” like robbery, drug abuse, violence or fornication. And then they struggle for decades with faults sins like laziness, unkindliness, vanity, impatience or judgmentality. What’s going on? It seems like at the outset they put away the bigger moral faults, and then they were left with smaller ones. Why is it that it takes so much longer to fight off the smaller ones? Why doesn’t it get easier, given that the faults are smaller? This is frustrating!
Instead, the experience sometimes seems to be like when you take a piece of unstretchable rope by two ends and pull. It is easy to get the initial big sag out. But as the sag gets smaller, it gets harder and harder to get it out.
Here is a thought. There are two ways of quantifying one’s moral state: the degree of vice and the degree of virtue. And the two are not related in a simple way, with one being the negation of the other. In ordinary circumstances, it doesn’t take much virtue to exclude murder from one’s life. But it does take a lot of virtue to exclude vanity from one’s life. To cease murdering is to lose much vice but is not to gain much virtue. To cease being vain, though, is not to lose much vice but it is to gain much virtue (is this true if one is still murdering, though?).
The “ordinary decent person” is perhaps not much more vicious than St. Teresa of Calcutta or St. Francis. But the “ordinary decent person” is far less virtuous.
Note that this is true even if we limit the discussion to what one might call “obligatory virtue”, i.e., the virtue that is opposed to vice rather than supererogatory virtue. The virtue involved in eliminating vanity is an obligatory virtue, though the virtue involved in giving up property for the sake of God and the poor, as St. Teresa and St. Francis did, is supererogatory. Yet the ordinary person is far less obligatorily virtuous than St. Teresa or St. Francis.
There may be an inverse relationship between vice and obligatory virtue: the more you have of the one, the less you have of the other. But a small increase of vice can correspond to large losses of virtue, and vice versa. It’s be a bit like that between the amount of sag in the rope and the horizontal force you need to push the ends with to balance the rope. As the sag goes to zero, the horizontal force goes to infinity.
The frustration I mentioned in the first paragraph then may be misplaced. For while it may seem like the moral life stalls after an initial burst of energy, the stalling may only be there if we measure the progress by the amount of vice. But if we measure by the amount of virtue, there might be steady increase throughout, just as a rope may linearly increase in tension, even though the sag seems not to be changing much.
(But may God have mercy on us!)
(While pushing metaphors perhaps too far, note that on the other hand the sag can’t go to infinity if the rope is unstretchable, since eventually we run out of rope. Likewise, perhaps, there is a limit to our vice, set by our nature. This fits with the idea of evil as a privation of the good.)
Thursday, September 28, 2017
Walking off to infinity
This is a simplified version of a paradox Josh Rasmussen sent me (“Rasmussen’s Rod”). Suppose that Laika is in a spaceship in a Euclidean non-relativistic space, and in one second she flies a kilometer, in the next half second another kilometer, and in the next quarter second another, and so on, all in exactly the same direction.
What will happen to Laika and the spaceship in two seconds?
Here are four answers:
Causal finitism: The story is impossible, as the outcome has infinitely many accelerations as causes.
Space is constituted by the relations between things in them rather than being a container. After two seconds, Laika will be infinitely far away from us. Where is that? It’s a place that didn’t exist until Laika got there, a place constituted by Laika’s being there and her distance from us.
Laika and the spaceship will leave space, and will exist as objects that aren’t externally spatial. (They might be internally spatial.)
Dogs and spaceships depend on space for their existence, and hence upon leaving they will cease to exist.
Tuesday, September 26, 2017
A causal finitist definition of the finite
Causal finitism says that nothing can have infinitely many causes. Interestingly, we can turn causal finitism around into a definition of the finite.
Say that a plurality of objects, the xs, is finite if and only if it possible for there to be a plurality of beings, the ys, such that (a) it is possible for the ys to have a common effect, and (b) it is possible for there to be a relation R such that whenever x0 one of the xs, then there is exactly one of a y0 among the xs such that Rx0y0.
Here's a way to make it plausible that the definition is extensionally correct if causal finitism is true. First, if the definition holds, then clearly there are no more of the xs than of the ys, and causal finitism together with (a) ensures that there are finitely many of the ys, so anything that the definition rules to be finite is indeed finite. Conversely, suppose the xs are a finite plurality. Then it should be possible for there to be a finite plurality of persons each of which thinks about a different one of the xs in such a way that each of the xs is thought about by one of the ys. Taking being thought about as the relation R makes the definition be satisfied.
Of course, on this account of finitude, causal finitism is trivial, for if a plurality of objects has an effect, then they satisfy the above definition if we take R to be identity. But what then becomes non-trivial is that our usual platitudes about the finite are correct.
Monday, September 25, 2017
Mathematical Platonist Universalism, consistency, and causal finitism
Mathematical Platonists say that sets and numbers exist. But there is a standard epistemological problem: How do we have epistemic access to the sets to the extent of knowing some of the axioms they satisfy? There is a solution to this epistemological problem, mathematical Platonist universalism (MPU): for any consistent collection of mathematical axioms, there are Platonic objects that satisfy these axioms. MPU looks to be a great solution to the epistemological problems surrounding mathematical Platonism. How did evolved creatures like us get lucky enough to have axioms of set theory or arithmetic that are actually true of the sets? It didn’t take much luck: As soon as we had consistent axioms, it was guaranteed that there would be a plurality of objects that satisfied them, and if the axioms fit with our “set intuitions”, we could call the members of any such plurality “sets” while if they fit with our “number intuitions”, we could call them “natural numbers”. And the difficult questions about whether things like the Axiom of Choice are true are also easily resolved: the Axiom of Choice is true of some pluralities of Platonic objects and is false of others, and unless we settle the matter by stipulation, no one of these pluralities is the sets. (The story here is somewhat similar to Joel Hamkins’ set theoretic multiverse, but I don’t know if Hamkins has the kind of far-reaching epistemological application in mind that I am thinking about.)
This story has a serious problem. It is surely only the consistent axioms that are satisfied by a plurality of objects. Axioms are consistent, by definition, provided that there is no proof of a contradiction from them. But proofs are themselves mathematical objects. In fact, we’ve learned from Goedel that proofs can be thought of as just numbers. (Just write your proof in ASCII, and encode it as a binary number.) Hence, a plurality of axioms is consistent if and only if there does not exist a number with a certain property, namely the property of encoding a proof of a contradiction from these axioms. But on MPU there is no unique plurality of mathematical objects deserving to be called “the numbers”. So now MPU faces a very serious problem. It said that any consistent plurality of axioms is true of some plurality of Platonic objects, and there are no privileged pluralities of “numbers” or “sets”. But consistency is itself defined by means of “the numbers”. And the old epistemological problems for Platonism resurface at this level. How do we have access to “the numbers” and the axioms they satisfy so as to have reason to think that the facts about consistency of axioms are as we think they are?
One could try making the same move again. There is no privileged notion of consistency. There are many notions of consistency, and for any axioms that are consistent with respect to any notion of consistency there exists a plurality of Platonic satisfiers. But now this literally threatens incoherence. But unless we specify some boundaries on the notion of consistency, this is going to literally let square circles into Platonic universalism. And if we specify the boundaries, then epistemological problems that MPU was trying to solve will come back.
At my dissertation defense, Robert Brandom offered a very clever suggestion for how to use my causal powers account of modality to account for provability: q can be proved from p provided that it is causally possible for someone to write down a proof of q from p. This can be used to account for consistency: axioms are consistent provided that it is not causally possible to write down a proof of a contradiction from them. There is a bit of a problem here, in that proofs must be finite strings of symbols, so one needs an account of the finite, and a plurality is finite if and only if its count is a natural number, and so this account seems to get us back to needing privileged numbers.
But if one adds causal finitism (the doctrine that only finite pluralities can together cause something) to the mix, we get a cool account of proof and consistency. Add the stipulation that the parts of a “written proof” need to have causal powers such that they are capable of together causing something (e.g., causing someone to understand the proof). Causal finitism then guarantees that any plurality of things that can work together to cause an effect is finite.
So, causal finitism together with the causal powers account of modality gives us a metaphysical account of consistency: axioms are consistent provided that it is not causally possible for someone to produce a written proof of a contradiction from them.
Friday, September 22, 2017
Free and responsible unconscious decisions
Whether a decision to do A is free and responsible does not depend on anything explanatorily posterior to the decision.
Our consciousness of x is always explanatorily posterior to x.
Hence, whether our decision to do A is free and responsible does not depend on our consciousness of having decided to do A.
If whether our decision to do A is free and responsible does not depend on our consciousness of having decided to do A, then it is possible to have a free and responsible unconscious decision to do A.
So, it is possible to have a free and responsible unconscious decision.
Let me, though, clarify something. This argument does not establish that the deliberation itself can be unconscious. It only establishes that one can be unconscious of the outcome of the deliberation. I suspect the deliberation can be unconscious as well, but I don't have as good an argument.
Two questions about sets
Here are two curious philosophical questions about set theory and its applicability outside mathematics.
Question 1: Suppose that every person has a perfectly well-defined mass. Is there a set of everybody mass, say the set of all real numbers x such that x is someone’s mass in kilograms?
The standard ZFC axioms are silent on this. They do say that for any predicate F in the language of set theory there is a set of all real numbers x satisfying F. But "mass" and "kilogram" are not parts of the language of set theory.
Question 2: What does it mean to say that there are finitely many horses?
An obvious answer is that if H is the set of all horses, then H is in one-to-one correspondence with some natural number. But the standard ZFC axioms only give us sets of sets, not sets of physical things like horses. If the correct set theory has ur-elements, elements that aren’t sets, maybe there is a set of all horses—but maybe not even then.
I suppose we could go metalinguistic. Begin by describing the set S of first-order logic sentences (sentences can be thought of as sets, even if sets are pure, i.e., have only sets as members) that say "There are no horses", "There is at most one horse", "There are at most two horses",.... And then say, using language beyond set theory, that at least one sentence in S is true.
But the metalinguistic approach won’t solve the seemingly related problem of what it means to say that there are countably many horses.
Progress report on books
My Necessary Existence book with Josh Rasmussen is right now in copyediting by Oxford.
I am making final revisions to the manuscript of Infinity, Causation and Paradox, with a deadline in mid October. As of right now, I've finished revising five out of ten chapters.
I am toying with one day writing a book on the ethics of love.
Thursday, September 21, 2017
Promising to sing infinitely many duets
Suppose you and I are going to live forever in heaven. I promise you that I will play sing a duet with you infinitely many times. Is this a valid promise?
Here is an argument that it is not. It seems that if the promise is valid, it generates reasons to sing duets with you. But it doesn’t. The reasons generated by a promise are reasons to do things that contribute to the fulfillment of the promise. But singing a duet with you does not contribute to the fulfillment of the promise. Here is one way to see this. Suppose I am considering whether to sing the duet with you on Wednesday, September 1, 2060. Consider now these two potential promises that I could imagine myself to have made:
I will sing a duet with you on infinitely many of the days that are not September 1, 2060.
I will sing a duet with you on infinitely many days.
Then singing the duet with you on September 1, 2060 does nothing to promote the fulfillment of promise (1). But (2) is logically equivalent to (1)! For I sing a duet with you on infinitely many days if and only if I sing a duet with you on infinitely many days that are not September 1, 2060. So my singing the duet on September 1, 2060 will no more promote the fulfillment of (2) than it will promote the fulfillment of (1). So, the promise doesn’t generate reasons to sing duets.
But things aren’t so simple. For while it doesn’t generate reasons to sing duets, it could generate reasons to do other things that bring about my singing duets with you on infinitely many days that are not September 1, 2060. For instance, here is something I could do: I could promise you to sing a duet with you every Wednesday for eternity. Making that promise will promote both (1) and (2). For the promise to sing duets on Wednesdays does unproblematically generate a reason to sing a duet on every Wednesday, and this generation of reasons is likely to contribute to my singing a duet with you on infinitely many days.
Of course, there are other promises I could make you that would make (1) and (2) likely. I could promise to sing a duet with you every January 1. Or every January 1 of a prime-numbered year. It’s a difficult question which of these promises I should make. But I have reason to make some such promise, or do something else that is likely to motivate me infinitely often, say inculcate a habit in myself.
So the answer to the initial question is plausibly positive. But it is only plausible if there is something other than singing duets that one can do in fulfillment of the promise. If all I am facing are the individual daily choices whether to sing a duet or not, without any habituation, I cannot validly promise to sing the duet on infinitely many occasions, as it would not generate any reasons.
A Trinitarian structure in love
On my view, love has a three-fold structure:
- benevolence
- appreciation
- union.
This three-fold structure has certain Trinitarian parallels. The Father is the benefactor: he gives being to the Son and thereby to the Holy Spirit. The Son admires the Father, is the Logos that reflects upon the Father’s goodness. The Holy Spirit unites the Father and the Son.
Wednesday, September 20, 2017
The Probabilistic Counterexampler
Every so often someone asks me if some piece of probabilistic reasoning works. For instance, today I got a query from a grad student whether
- P(A|C)>P(A|B) implies P(A|B ∨ C)>P(A|B).
Of course, I could think about it each time somebody asks me something. But why think when a computer can solve a problem by brute force?
So, last spring I wrote a quick and dirty python program that looks for counterexamples to questions like that simply by considering situations with three dice, and iterating over all the possible combinations of subsets A, B and C of the state space (with some reduction due to symmetries).
The program is still quick and dirty, but at least I made the premises and conclusions not be hardcoded. You can get it here.
For instance, for the query above, you can run:
python probab-reasoning.py "P(a,c)>P(a,b)" "P(a,b|c)>P(a,b)" (The vertical bars are disjunction, not conditional probability. Conditional probability uses commas.) The result is:
a={1}, b={1, 2}, c={1}
a={1}, b={1, 2, 3}, c={1}
a={1}, b={1, 2, 3}, c={1, 2}
a={1}, b={1, 2, 3}, c={1, 3}
a={1}, b={1, 2, 3}, c={1, 4}
...So, lots of counterexamples. On the other hand, you can do this:
python probab-reasoning.py "P(a)*P(b)==P(a&b)" "P(b)>0" "P(a,b)==P(a)" and it will tell you no counterexamples were found. Of course, that doesn’t prove that the result is true, but in this case it is.
The general operation is that you install python (either 2.7 or 3.x) and use a commandline to run:
python probab-reason.py premise1 premise2 ... conclusionsYou can use any single letter variables for events, other than P, and the operations & (conjunction), | (disjunction) and ~ (negation) between the events. You can use conditional probability P(a,b) and unconditional probability P(a). You can use standard arithmetical and comparison operators on probabilities. Make sure that you use python’s operators. For instance, equality is ==, not =. You should also use python’s boolean operations when you are not working with events: e.g., “P(a)==1 and P(b)==0.5”.
Any premise or conclusion that requires conditionalization on a probability zero event to evaluate automatically counts as false.
You can use up to five single-letter variables and you can also specify the number of sides the die has prior to listing the premises. E.g.:
python probab-reasoning.py 8 "P(a)*P(b)==P(a&b)" "P(b)>0" "P(a,b)==P(a)" Monday, September 18, 2017
Two ways of being vicious
Many of the times when Hitler made a wrong decision, his character thereby deteriorated and he became more vicious. Let’s imagine that Hitler was a decent young man at age 19. Now imagine Schmitler, who lived a life externally just like Hitler’s, but on Twin Earth. Until age 19, Schmitler’s life was just like Hitler. But from then on, each time Schmitler made a wrong choice, aliens or angels or God intervened and made sure that the moral deterioration that normally follows upon wrong action never occurred. As it happens, however, Schmitler still made the same choices Hitler did, and made them with freedom and clear understanding of their wickedness.
Thus, presumably unlike Hitler, Schmitler did not morally fall, one wrong action at a time, to the point of a genocidal character. Instead, he committed a series of wrong actions, culminating in genocide, but each action was committed from the same base level of virtue and vice, the same level that both he and Hitler had at age 19. This is improbable, but in a large enough universe all sorts of improbable things will happen.
So, now, here is the oddity. Since Schmitler’s level of virtue and vice at the depth of his moral depradations was the same as at age 19, and at age 19 both he and Hitler were decent young men (or so I assume), it seems we cannot say that Schmitler was a vicious man even while he was committing genocidal atrocities. And yet Schmitler was fully responsible for these atrocities, perhaps more so than Hitler.
I want to say that Schmitler is spectacularly vicious without having much in the way of vices, indeed while having more virtue than vice (he was, I assume, a decent young man), even though that sounds like a contradiction. Schmitler is spectacularly vicious because of what he has done.
This doesn’t sound right, though. Actions are episodic. Being vicious is a state. Hitler was a vicious man while innocently walking his dog on a nice spring day in 1944, even when not doing any wrongs. And we can explain why Hitler was vicious then: he had a character with very nasty vices, even while he was not exercising the vices. But how can we say that Schmitler was vicious then?
Here’s my best answer. Even on that seemingly innocent walk, Schmitler and Hitler were both failing to repent of their evil deeds, failing to set out on the road of reconciliation with their victims. A continuing failure to repent is not something episodic, but something more like a state.
If this is right, then there are two ways of being vicious: by having vices and by being an unrepentant evildoer.
(A difficult question Robert Garcia once asked me is relevant, though: What should we say about people who have done bad things but suffered amnesia?)
Some arguments about the existence of a good theodicy
This argument is valid:
If no good theodicy can be given, some virtuous people’s lives are worthless.
No virtuous person’s life is worthless.
So, a good theodicy can be given.
The thought behind 1 is that unless we accept the sorts of claims that theodicists make about the value of virtue or the value of existence or about an afterlife, some virtuous people live lives of such great suffering, and are so far ignored or worse by others, that their lives are worthless. But once one accepts those sorts of claims, then a good theodicy can be given.
Here is an argument for 2:
It would be offensive to a virtuous person that her life is worthless.
The truth is not offensive to a virtuous person.
So, no virtuous person’s life is worthless.
Perhaps, too, an argument similar to Kant’s arguments about God can be made. We ought to at least hope that each virtuous person’s life has value on balance. But to hope for that is to hope for something like a theodicy. So we ought to hope for something like a theodicy.
The above arguments may not be all that compelling. But at least they counter the argument in the other direction, that it is offensive to say that someone’s sufferings have a theodicy.
Here is yet another argument.
That there is no good theodicy is an utterly depressing claim.
One ought not advocate utterly depressing claims, without very strong moral reason.
There is no very strong moral reason to advocate that there is no good theodicy.
So, one ought not advocate that there is no good theodicy.
The grounds for 8 are pragmatic: utterly depressing claims tend to utterly depress people, and being utterly depressed is very bad. One needs very strong reason to do something that causes a very bad state of affairs. I suppose the main controversial thesis here is 9. Someone who thinks religion is a great evil might deny 9.
Let's not exaggerate the centrality of virtue to ethics
Virtues are important. They are useful: they internalize the moral law and allow us to make the right decision quickly, which we often need to do. They aren’t just time-savers: they shine light on the issues we deliberate over. And the development of virtue allows our freedom to include the two valuable poles that are otherwise in tension: (a) self-origination (via alternate possibilities available when we are developing virtue) and (b) reliable rightness of action. This in turn allows our development of virtue reflect the self-origination and perfect reliability in divine freedom.
But while virtues are important, they are not essential to ethics. We can imagine beings that only ever make a single, but truly momentous, decision. They come into existence with a clear understanding of the issues involved, and they make their decision, without any habituation before or after. That decision could be a moral one, with a wrong option, a merely permissible option, and a supererogatory option. They would be somewhat like Aquinas’ angels.
We could even imagine beings that make frequent moral choices, like we do, but whose nature does not lead them too habituate in the direction of virtue or vice. Perhaps throughout his life whenever Bill decides whether to keep an onerous promise or not, there is a 90% chance that he will freely decide rightly and a 10% chance that he will freely decide wrongly, a chance he is born and dies with. A society of such beings would be rather alien in many practices. For instance, members of that society could not be held responsible for their character, but only for their choices. Punishment could still be retributive and motivational (for the chance of wrong action might go down when there are extrinsic reasons against wrongdoing). I think such beings would tend to have lower culpability for wrongdoing than we do. For typically when I do wrong as a middle-aged adult, I am doubly guilty for the wrong: (a) I am guilty for the particular wrong choice that I made, and (b) I am guilty for not having yet transformed my character to the point where that choice was not an option. (There are two reasons we hold children less responsible: first, their understanding is less developed, and, second, they haven’t had much time to grow in virtue.)
Nonetheless, while such virtue-less beings woould be less responsible, and we wouldn’t want to be them or live among them, they would still have some responsibility, and moral concepts could apply to them.
Saturday, September 16, 2017
Adding a USB charging port to an elliptical machine
Friday, September 15, 2017
Four-dimensionalism and caring about identity

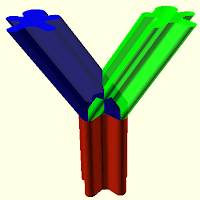
This view seems to me to be deeply implausible from a four-dimensional point of view. I am a four-dimensional thing. This four-dimensional thing should prudentially care about what happens to it, and only about what happens to it. The red-and-black four-dimensional thing in the diagram here (up/down represents time; one spatial dimension is omitted) should care about what happens to the red-and-black four-dimensional thing, all along its temporal trunk. This judgment seems completely unaffected by learning that the dark slice represents an episode of amnesia, and that no memories pass from the bottom half to the upper half.
 Or take a case of symmetric fission, and suppose that the facts of identity are such that I am the red four-dimensional thing in the diagram on the right. Suppose both branches have full memories of what happens before the fission event. If I am the red four-dimensional thing, I should prudentially care about what happens to the red four-dimensional thing. What happens to the green thing on the right is irrelevant, even if it happens to have in it memories of the pre-split portion of me.
Or take a case of symmetric fission, and suppose that the facts of identity are such that I am the red four-dimensional thing in the diagram on the right. Suppose both branches have full memories of what happens before the fission event. If I am the red four-dimensional thing, I should prudentially care about what happens to the red four-dimensional thing. What happens to the green thing on the right is irrelevant, even if it happens to have in it memories of the pre-split portion of me.The same is true if the correct account of identity in fission is Parfit’s account, on which one perishes in a split. On this account, if I am the red four-dimensional person in the diagram on the left, surely I should prudentially care only about what happens to the red four-dimensional thing; if I am the green person, I should prudentially care only about what happens to the green one; and if I am the blue one, I should prudentially care only about what happens to the blue one. The fact that both the green and the blue people remember what happened to the red person neither make the green and blue people responsible for what the red person did nor make it prudent for the red person to care about what happens to the green and blue people.
This four-dimensional way of thinking just isn’t how the discussion is normally phrased. The discussion is normally framed in terms of us finding ourselves at some time—perhaps a time before the split in the last diagram—and wondering which future states we should care about. The usual framing is implicitly three-dimensionalist: what should I, a three-dimensional thing at this time, prudentially care about?
But there is an obvious response to my line of thought. My line of thought makes it seem like I am transtemporally caring about what happens. But that’s not right, not even if four-dimensionalism is true. Even if I am four-dimensional, my cares occur at slices. So on four-dimensionalism, the real question isn’t what I, the four-dimensional entity, should prudentially care about, but what my three-dimensional slices, existent at different times, should care about. And once put that way, the obviousness of the fact that if I am the red thing, I should care about what happens to the red thing disappears. For it is not obvious that a slice of the red thing should care only about what happens to other slices of the red thing. Indeed, it is quite compelling to think that the psychological connections between slices A and B matter more than the fact that A and B are in fact both parts of the same entity. (Compare: the psychological connections between me and you would matter more than the fact that you and I are both parts of the same nation, say.) The correct picture is the one here, where the question is whether the opaque red slice should care about the opaque green and opaque blue slices.
In fact, in this four-dimensionalist context, it’s not quite correct to put the Parfit view as “psychological connections matter more than identity”. For identity doesn’t obtain between different slices. Rather, what obtains is co-parthood, an obviously less significant relation.
However, this response to me depends on a very common but wrongheaded version of four-dimensionalism. It is I that care, feel and think at different times. My slices don’t care, don’t feel and don’t think. Otherwise, there will be too many carers, feelers and thinkers. If one must have slices in the picture (and I don’t know that that is so), the slices might engage in activities that ground my caring, my feeling and my thinking. But these grounding activities are not caring, feeling or thinking. Similarly, the slices are not responsive to reasons: I am responsive to reasons. The slices might engage in activity that grounds my responsiveness to reasons, but that’s all.
So the question is what cares I prudentially should have at different times. And the answer is obvious: they should be cares about what happens to me at different times.
About the graphics: The images are generated using mikicon’s CC-by-3.0 licensed Gingerbread icon from the Noun Project, exported through this Inkscape plugin and turned into an OpenSCAD program (you will also need my tubemesh library).
Thursday, September 14, 2017
Agents, patients and natural law
Thanks to Adam Myers’ insightful comments, I’ve been thinking about the ways that natural law ethics concerns natures in two ways: on the side of the agent qua agent and on the of the patient qua patient.
Companionship is good for humans and bad for intelligent sharks, let’s suppose. This means that we have reasons to promote companionship among humans and to hamper companionship among intelligent sharks. That’s a difference in reasons based on a difference in the patients’ nature. Next, let’s suppose that intelligent sharks by nature have a higher degree of self-concern vs. other-concern than humans do. Then the degree to which one has an obligation to promote the very same good–say, the companionship of Socrates–will vary depending on whether one is human or a shark. That’s a difference in reasons based on a difference in the agents’ nature.
I suspect it would make natural law ethics clearer if natural lawyers were always clear on what is due to the agent’s nature and what is due to the patient’s nature, even if in fact their interest were solely in cases where the agent and patient are both human.
Consider, for instance, this plausible thesis:
- I should typically prioritize my understanding over my fun.
Suppose the thesis is true. But now it’s really interesting to ask if this is true due to my nature qua agent or my nature qua patient. If I should prioritize my understanding over my fun solely because of my nature qua patient, then we could have this situation: Both I and an alien of some particular fun-loving sort should prioritize my understanding over my fun, but likewise both I and the alien should prioritize the alien’s fun over the alien’s understanding, since human understanding is more important than human fun, while the fun of a being like the alien is more important than the understanding of such a being. On this picture, the nature of the patient specifies which goods are more central to a patient of that nature. On the other hand, if I should prioritize my understanding over my fun solely because of my nature qua agent, then quite possibly we are in the interesting position that I should prioritize my understanding over my fun, but also that I should prioritize the alien’s understanding over the alien’s fun, while the alien should prioritize both its and my fun over its and my understanding. For me promoting understanding is a priority while for the alien promoting fun is a priority, regardless of whose understanding and fun they are.
And of course we do have actual and morally relevant cases of interaction across natures:
God and humans
Angels and humans
Humans and brute animals.
Wednesday, September 13, 2017
Probabilities and Boolean operations
When people question the axioms of probability, they may omit to question the assumptions that if A and B have a probability, so do A-or-B and A-and-B. (Maybe this is because in the textbooks those assumptions are often not enumerated in the neat lists of the “three Kolmogorov axioms”, but are given in a block of text in a preamble.)
First note that as long as one keeps the assumption that if A has a probability, so does not-A, then by De Morgan’s, any counterexample to conjunctions having a probability will yield a counterexample to disjunctions having a probability. So I’ll focus on conjunctions.
I’m thinking that there is reason to question these axioms, in fact two reasons. The first reason, one that I am a bit less impressed with, is that limiting frequency frequentism can easily violate these two axioms. It is easy to come up with cases where A-type events have a limiting frequency, B-type ones do, too, but (A-and-B)-type ones don’t. I’ve argued before that so much the worse for frequentism, but now I am not so sure in light of the second reason.
The second reason is cases like this. You have an event C that has no probability whatsoever–maybe it’s an event of a dart hitting a nonmeasurable set–and a fair indeterministic coin flip causally independent of C. Let H and T be the events of the coin flip being heads or tails. Then let A be the event:
- (H and C) or (T and not C).
Here’s an argument that P(A)=1/2. Imagine a coin with erasable heads and tails images, and imagine that a trickster prior to flipping a coin is going to decide, using some procedure or other, whether to erase the heads and tails images on the coin and draw them on the other side. “Clearly” (as we philosophers say when we have no further argument!) as long as the trickster has no way of seeing the future, the trickster’s trick will not affect the probabilities of heads or tails. She can’t make the coin be any less or more likely to land heads by changing which side heads lies on. But that’s basically what’s going on in A: we are asking what the probability of heads is, with the convention that if C doesn’t happen, then we’ll have relabeled the two sides.
Another argument that P(A)=1/2 is this (due to a comment by Ian). Either C happens or it doesn’t. No matter which is the case, A has a chance 1/2 of happening.
So A has probability 1/2. But now what is the probability of A-and-H? It is the same as the probability of C-and-H, which by independence is half of the probability of C, and the latter probabilit is undefined. Half of something undefined is still undefined, so A-and-H has an undefined probability, even though A has a perfectly reasonable probability of 1/2.
A lot of this is nicely handled by interval-valued theories of probability. For we can assign to C the interval [0, 1], and assign to H the sharp probability [1/2, 1/2], and off to the races we go: A has a sharp probability as does H, but their conjunction does not. This is good motivation for interval-valued theories of probability.
Tuesday, September 12, 2017
Numerical experimentation and truth in mathematics
Is mathematics about proof or truth?
Sometimes mathematicians perform numerical experiments with computers. Goldbach’s Conjecture says that every even integer n greater than two is the sum of two primes. Numerical experiments have been performed that verified that this is true for every even integer from 4 to 4 × 1018.
Let G(n) be the statement that n is the sum of two primes, and let’s restrict ourselves to talking about even n greater than two. So, we have evidence that:
- For an impressive sample of values of n, G(n) is true.
This gives one very good inductive evidence that:
- For all n, G(n) is true.
And hence:
- It is true that: for all n, G(n). I.e., Goldbach’s Conjecture is true.
Can we say a similar thing about provability? The numerical experiments do indeed yield a provability analogue of (1):
- For an impressive sample of values of n, G(n) is provable.
For if G(n) is true, then G(n) is provable. The proof would proceed by exhibiting the two primes that add up to n, checking their primeness and proving that they add up to n, all of which can be done. We can now inductively conclude the analogue of (2):
- For all n, G(n) is provable.
But here is something interesting. While we can swap the order of the “For all n” and the “is true” operator in (2) and obtain (3), it is logically invalid to swap the order of the “For all n” and the “is provable” operator (5) to obtain:
- It is provable that: for all n, G(n). I.e., Goldbach’s Conjecture is provable.
It is quite possible to have a statement such that (a) for every individual n it is provable, but (b) it is not provable that it holds for every n. (Take a Goedel sentence g that basically says “I am not provable”. For each positive integer n, let H(n) be the statement that n isn’t the Goedel number of a proof of g. Then if g is in fact true, then for each n, H(n) is provably true, since whether n encodes a proof of g is a matter of simple formal verification, but it is not provable that for all n, H(n) is true, since then g would be provable.)
Now, it is the case that (5) is evidence for (6). For there is a decent chance that if Goldbach’s conjecture is true, then it is provable. But we really don’t have much of a handle on how big that “decent chance” is, so we lose a lot of probability when we go from the inductively verified (5) to (6).
In other words, if we take the numerical experiments to give us lots of confidence in something about Goldbach’s conjecture, then that something is truth, not provability.
Furthermore, even if we are willing to tolerate the loss of probability in going from (5) to (6), the most compelling probabilistic route from (5) to (6) seems to take a detour through truth: if G(n) is provable for each n, then Goldbach’s Conjecture is true, and if it’s true, it’s probably provable.
So the practice of numerical experimentation supports the idea that mathematics is after truth. This is reminiscent to me of some arguments for scientific realism.
Presentism and multiverses
It is possible to have an island universe whose timeline has no temporal connection to our timeline.
If presentism is true, it is not possible to have something that has no temporal connection to our timeline.
So, presentism is not true.
Presentism and classical theism
If presentism is true, then everything that exists, exists presently.
Anything that exists presently is temporal.
God exists.
So, if presentism is true, then God is temporal.
But God is not temporal.
So, presentism is not true.
Some presentists will be happy to embrace the thesis that God is temporal. But what about presentist classical theists? I suppose they will have to deny (1). Maybe they can replace it with:
- If presentism is true, then everything temporal that exists, exists presently.
Presentism is now longer an elegant thesis about the nature of existence, though.
Maybe a better move for the presentist is to deny (2)? There is some reason to do that. God while not being spatial is everywhere. Similarly God is everywhen, and hence he is in the present, too. But I am not sure if being in the present is the same as existing presently.
Monday, September 11, 2017
Supertasks and empirical verification of non-measurability
I have this obsession with probability and non-measurable events—events to which a probability cannot be attached. A Bayesian might think that this obsession is silly, because non-measurable events are just too wild and crazy to come up in practice in any reasonably imaginable situation.
Of course, a lot depends on what “reasonably imaginable” means. But here is something I can imagine, though only by denying one of my favorite philosophical doctrines, causal finitism. I have a Thomson’s Lamp, i.e., a lamp with a toggle switch that can survive infinitely many togglings. I have access to it every day at the following times: 10:30, 10:45, 10:52.5, and so on. Each day, at 10:00 the lamp is off, and nobody else has access to the machine. At each time when I have access to the lamp, I can either toggle or not toggle its switch.
I now experiment with the lamp by trying out various supertasks (perhaps by programming a supertask machine), during which various combinations of toggling and not toggling happen. For instance, I observe that if I don’t ever toggle the switch, the lamps stays off. If I toggle it a finite number of times, it’s on when that number is odd and off when that number is even. I also notice the following regularities about cases where an infinite number of togglings happens:
The same sequence (e.g., toggle at 10:30, don’t toggle at 10:45, toggle at 10:52.5, etc.) always produces the same result.
Reversing a finite number of decisions in a sequence produces the same outcome when an even number of decisions is reversed, and the opposite outcome when an odd number of decisions is reversed.
(Of course, 1 is a special case of 2.) How fun! I conclude that 1 and 2 are always going to be true.
Now I set up a supertask machine. It will toss a fair coin just prior to each of my lamp access times, and it will toggle the switch if the coin is heads and not toggle it if it is tails.
Question: What is the probability that the lamp will be on at 11?
“Answer:” Given 1 and 2, the event that the lamp will be on at 11 is not measurable with respect to the standard (completed) product measure on a countable infinity of coin tosses. (See note 1 here.)
So, given supertasks (and hence the falsity of causal finitism), we could find ourselves in a position where we would have to deal with a non-measurable set.
Natural law love-first metaethics
Start with this Aristotelian thought:
- Everything should to fulfill its nature, and every “should” fact is a norm specifying the norm of fulfilling one’s nature.
But not every “should” is a moral should. Sheep should have four legs, but a three-legged sheep is not morally defective. Here’s a hypothesis:
- A thing morally should A if and only if that thing has a will with an overriding norm of loving everything and that the thing morally should A is a specification of that norm.
On this theory, moral norms are norms for the same Aristotelian reason that all other norms are norms—all norms derive from the natures of things. But at the same time, the metaethics is a metaethics of love. What renders a norm a moral norm is its content, that it is a specification of the norm that one should love everything.
Why is it, on this theory, that I should be affable to my neighbor? Because such affability is a specification of the norm of fulfilling my nature. But that needn’t be my practical reason for the affability: rather, that is the explanation of why I should be affable (cf. this). What makes the norm of affability to my neighbor a moral norm? That I have a norm of love of everything, and that the norm of affability specifies that norm.
And we can add:
- A thing is a moral agent if and only if it has a will with an overriding norm of loving everything.
One could, perhaps, imagine beings that have a will with an overriding norm of self-benefit. Such beings wouldn’t be moral agents. But we are moral agents. In fact, I suspect the following is true:
- Loving everything is the only proper function of the human will.
Given the tight Aristotelian connection between proper function and norms:
- All norms on the human will are specifications of the norm of loving everything.
This metaethical theory I think is both a natural law theory and a love-first metaethics. It is a natural law theory in respect of the sources of normativity, and it is a love-first metaethics in respect of the account of moral norms. Thus it marries Aristotle with the Gospel, which is a good thing. I kind of like this theory, though I have a nagging suspicion it has problems.
Reductive accounts of matter
I’ve toyed with identifying materiality with spatiality (much as Descartes did). But here’s another very different reductive idea. Maybe to be material is to have energy. Energy on this view is a physical property, maybe a functional one and maybe a primitive one.
If this view is right, then one might have worlds where there are extended objects in space, but where there is no matter because the physics of these objects is one that doesn’t have room or need for energy.
Note that the sense of “matter” involved here is one on which fields, like the electromagnetic one, are material. I think that in the philosophical usage of “material” and “matter”, this is the right answer. If it turned out that our minds were identical with the electromagnetic fields in our brains, that would surely be a vindication of materialism rather than of dualism.
Now, here’s something I’m worrying about when I think about matter, at least after my rejection of Aristotelian matter. There seem to be multiple properties that are co-extensive with materiality in our world:
spatiality
energy
subjection to the laws of physics (and here there are two variants: subjection to our laws of physics, and subjection to some laws of physics or other; the latter might be circular, though, because maybe “physics” is what governs matter?).
Identifying matter with one or more of them yields a different concept of materiality, with different answers to modal questions. And now I wonder if the question of what matter is is a substantive one or a merely verbal one? On the Aristotelian picture, it was clearly a substantive question. But apart from that picture, it’s looking more and more like a merely verbal question to me.
Non-measurable sets and intuition
Here’s an interesting reason to accept the existence of non-measurable sets (and hence of whatever weak version of the Axiom of Choice that it depends on). A basic family of mathematical results in analysis says that most measurable real-valued functions on the real line are “close to” being continuous, i.e., that they can be approximated by continuous functions in some appropriate sense. But it is intuitive to think that there “should” be real-valued functions on the real line that are not close to being continuous—there “should” be functions that are very, very messy. So, intuitively, there should be non-measurable functions, and hence non-measurable sets.
Friday, September 8, 2017
A defense of natural law eudaimonism
My main objection to natural law ethics has for a long time been that it looks egoistic because it is eudaimonistic. One version of that worry is the “one thought too many” objection: You should just do good to your fellow humans because they are who they are, because they are your fellow human beings, or something like that, but definitely not because doing so leads to your flourishing.
I think there is a nice—and probably well-known to people other than me—response to this version of the worry, and to many similar “one thought too many” worries. To put this “one thought too many” worry more abstractly, the worry is that the metaethics will infect the reasons for action in an unacceptable way. But the response should simply be that, first, what metaethics asks is this question:
- What makes the reasons for action be reasons for action?
Here, read “reasons” factively as “good reasons” or even “good moral reasons” (I don’t actually distinguish the two, but many do), not as motivations. And, second, insofar as R is my reason for my action, I am acting on account of R, not on account of R being a reason. Compare: what causes the fire is the match, not the match’s being a cause.
Thus, the natural lawyer should say that what makes the fact that an action promotes the good of my neighbor be a reason is that I flourish (in part) by intentionally (under this description) promoting the good of my neighbor. But the reason for the action is that the action promotes the good of my neighbor, not that I flourish by intentionally promoting the good of my neighbor. The natural law answer to the metaethics question (1) is this:
- R is on balance a reason for action if and only if, and if so then because, I flourish by acting on R.
We do in fact flourish by intentionally promoting the good of our neighbor. Note that (2) does not by itself yield any egoism in our motivations. We could imagine selfless beings that flourish only insofar as they are intentionally promoting the good of their neighbor as a final end, and who are blighted insofar as they are intentionally promoting their own good or flourishing. We are, of course, not such selfless beings, but we don’t learn the fact that we are not such beings from (2). In fact, (2) is fully logically compatible with us being such beings. Hence, the metaethical theory (2) cannot by itself give rise to the “one thought too many” worry I started the post with. (Of course, some natural lawyers will go beyond (2). They may say that in fact our happiness is the end of all our actions. If so, then I think they are subject to the “one thought too many” worry.)
It is important to add a little bit to the above story. While it is true that “this benefits my friend” is typically reason enough, and that I don’t need to act on the second order fact that “this benefitting my friend is a reason”, we also do have such second order reasons. That there is a reason for an action is itself a reason for action. A parent might tell a child: “You have good reason to do this, but I can’t explain the reason right now.” In that case, the child could well be acting on the second-order reason that there is a first-order reason. (The child could also be acting on a first-order reasons to please the parent).
Here is another kind of case. I start off without any belief about whether R is a reason for action, and R leaves me cold. Maybe I am completely insensitive to considerations of privacy, and the fact that an action promotes someone’s privacy just leaves me completely cold. But I observe my virtuous friends, and see that they are acting on reasons like R, and I notice that their so acting contributes to what I admire about them. I conclude that R is in fact a good reason for action. But that’s purely intellectual. I am still left quite cold and unmotivated by the fact that some proposed action A falls under R. But what I can do at this point is to act on the second-order reason that A falls under a good reason. I can even say what that good reason is. But I cannot act on it itself, because it leaves me cold.
These are, however, non-ideal cases. If I know that R is a good reason, I should strive to form my will to be motivated by R. It will be better to act on R than to act on the knowledge that R is a reason. And thinking about these cases makes the response to the “one thought too many” worry about natural law even more compelling, I think. It does promote my flourishing to promote my flourishing, though I think that it doesn’t promote my flourishing as well as promoting the flourishing of others does. So that kindliness to others promotes my flourishing is a reason for benefiting others, just not as good a reason as that it benefits others. But such “not as good reasons” are important for our moral development: we are not yet in the ideal state, and so that “one thought too many” is still needed.
This helps make me feel a lot better about natural law ethics. Not quite enough to embrace it, though.
Thursday, September 7, 2017
Two kinds of non-measurable events
Non-measurable events are ones to which the probability function in the situation assigns no probability. Philosophically speaking, non-measurable events come in two varieties:
Non-measurable events that should not have any probability assignment.
Non-measurable events that should have a probability assignment.
Type (1) non-measurable events are the kinds of weird events that can be constructed from the Hausdorff and Banach-Tarski paradoxes, as well as perhaps (this is less clear) the Vitali non-measurable sets.
But I think there are also type (2) non-measurable events relative to standard choices of probability functions. For instance, suppose that in each universe of an infinite multiverse a fair coin is tossed countably infinitely often.
How likely is it that in at least one universe all the coin tosses are heads? If the universes form a countable infinity, classical probability theory gives an answer: zero. But if the universes form an uncountable infinity, classical probability theory gives no answer at all—the standard completed product measure makes the event be non-measurable. However, intuitively, there should be an answer in at least some cases. If the number of universes is much larger than the number of possible countable sequences of coin tosses (i.e., is much larger than 2ω), we would expect the probability to be 1 or close to it. We can coherently extend the standard probability function to give that answer. But we can also coherently extend it to give a different answer, including the answer that the probability of an all-heads universe is zero, even if the number of universes is a gigantic infinite cardinality.
We don’t want to just make up an answer here. We want the answer to be derivable in some way resembling the proof of the theorem that if you toss a coin infinitely many times, you’ve got probability 1 of getting heads at least once.
I suppose we could take it to be a metaphysical axiom that if you have K disjoint collections each with M coin tosses, then if K and M are infinite and K > M, then with probability one at least one collection yields all heads. But it would be nice to have more than just intuition here, and in similar problems.
Wednesday, September 6, 2017
A problem for some Humeans
Suppose that a lot of otherwise ordinary coins come into existence ex nihilo for no cause at all. Then whether a given coin lies heads or tails up is independent of how all the other coins lie in the sense that no information about the other coins will give you any data about how this one lies.
It is crucial here that the coins came into existence causelessly. If the coins came off an assembly line, and a large sample were all heads-up, we would have good reason to think that the causal process favored that arrangement and hence that the next coin to be examined will also be heads-up.
But now suppose that I know that Humeanism about laws is true, and there is a very, very large number of coins lying in a pile, all of which I know for sure to have come to be there causelessly ex nihilo, and there are no other coins in the universe. Suppose, further, that in fact all the coins happen to lie heads-up. Then when the number of coins is sufficiently large (say, of the order of magnitude of the number of particles in the universe), on Humean grounds it will be a law of nature that coins begin their existence in the heads-up orientation. But if the independence thesis I started the post with is true, then no matter how many coins I examined, I would not have any more reason to think that the next unexamined coin is heads than that it is tails. Thus, in particular, I would not be justified in believing in the heads-up law.
One might worry that I couldn’t know, much less know for sure, that the coins are there causelessly ex nihilo. A reasonable inference from the fact that lots of examined coins are all heads-up would seem to be that they were thus arranged by something or someone. And if I made that inference, then I could reasonably conclude that the coins are all heads-up. But my conclusion, while true and justified, would not be knowledge. I would be in a Gettier situation. My justification depends essentially on the false claim that the coins were arranged by something or someone. So even if one drops the assumption that I know that the coins are there causelessly ex nihilo, I still don’t know that the heads-up law holds. Moreover, my reason for not knowing this has nothing to do with dubious theses about the infallibility of knowledge. I don’t know that the heads-up law holds, whether fallibly or infallibly.
There is no problem for the Humean as yet. After all, there is nothing absurd about there being hypothetical situations where there is a law but we can’t know that it obtains. But for any Humean who additionally thinks that our universe came into existence causelessly, there is a real challenge to explain why the laws of our world are not like the heads-up law—laws that we cannot know from a mere sample of data.
This problem is fatal, I think, to the Humean who thinks that our universe started its existence with a large number of particles. For the properties of the particles would be like the heads-up and tails-up orientations of the coins, and we would not be in a position to know all particles fall into some small number of types (as the standard model in particle physics does). But a Humean scientist who doesn’t think the universe has a cause could also think that our universe started its existence with a fairly simple state, say a single super-particle, and this simple state caused all the multitude of particles we observe. In that case, the order-in-multiplicity that we observe would not be causeless, and the above argument would not apply.