Being mistaken about what you believe

Consider:

1. I don’t believe (1).

Add that I am opinionated on what I believe:

2. For each proposition p, I either believe that I believe p or believe that I do not believe p.

Finally, add:

3. My beliefs are closed under entailment.

Now I either believe (1) or not. If I do not believe (1), then I don’t believe that I don’t believe (1), by closure. But thus, by (2), I do believe that I do believe (1). Hence in this case:

4. I am mistaken about what I do or do not believe.

Now suppose I do believe (1). Then I believe that I don’t believe (1), by closure and by what (1) says. So, (4) is still true.

Thus, we have an argument that if I am opinionated on what I believe and my beliefs are closed under entailment, then I am mistaken as to what I believe.

(Again, we need some way of getting God out of this paradox. Maybe the fact that God’s knowledge is non-discursive helps.)

Closure for credence thresholds is atypical

In an earlier post, I speculated about thresholds and closure without doing any calculations. Now it’s time to do some calculations.

The Question: If you have two propositions that meet a credential threshold, how likely is it that their conjunction does as well? I.e., how likely is closure to hold for pairs of propositions meeting the threshold?

Model 1: Take a probability space with N points. Assign a credence to each of the N points by uniformly choosing a random number in some fixed range, and then normalizing so total probability is 1. Now among the 2^N (up to equivalence) propositions about points in the probability space, choose two at random subject to the constraint that they both meet the threshold condition. Check if their conjunction meets the threshold condition. Repeat. The source code is here (MIT license).

The Results: With thresholds ranging from 0.85 to 0.95, as N increases, the probability of the conjunction meeting the threshold goes down. At N = 16, for all three thresholds, it is below 0.5. At N = 24, for all three thresholds, it is below 0.21. In other words, for randomly chosen propositions, we can expect closure to be atypical.

Note: The original model allows the two random propositions to turn out to be the same one. Otherwise, for N such that 1/N < t₀, where t₀ is the threshold, the probability of closure could be undefined as it might be impossible to generate two distinct propositions that meet the closure condition. Dropping the condition that allows the two random propositions to be the same will only make the probability of closure smaller. Here (also MIT license) is the modified code that does this. The results are here.

Final Remarks: This suggests that if the justification condition for knowledge is expressed in terms of a credence threshold, closure for knowledge will be atypical: i.e., for a random pair of propositions one knows, it will be unlikely that one will know the conjunction. Of course, it could be that the other conditions for knowledge, besides justification, will affect this, by making closure somewhat more likely. But I don’t have reason to think it will make an enormous difference. So, if one thinks closure should be typical, one shouldn’t think that justification is described by a credence threshold.

I go the other way: I think justification is described by a credence threshold, and now I think that closure is unlikely to be typical.

A limitation in the above models is that the propositions we normally talk about are not randomly chosen from the 2^N propositions describing the probability space.

Conjunctions and thresholds

Consider some positive epistemic or doxastic concept E, say knowledge or belief. Suppose that (maybe for a fixed context) E requires a credence threshold t₀: a proposition only falls under E when the credence is t₀ or higher.

Unless the non-credential stuff really, really cooperates, we wouldn’t expect to have closure under conjunction for all cases of E. For if p and q are cases of E that just barely satisfy the credential threshold condition, we wouldn’t expect their conjunction to satisfy it.

Question: Do we have any right to expect closure under conjunction typically, at least with respect to the credential condition? I.e., if p and q are randomly chosen distinct cases of E, is it reasonable to expect that their conjunction falls above the threshold?

Simple Model: The credences of our Es can fall anywhere between t₀ and 1. Let’s suppose that the distribution of the credences is uniform between t₀ and 1. Suppose, two, that distinct Es are statistically independent, so that the probability of the conjunction is the product of the probabilities.

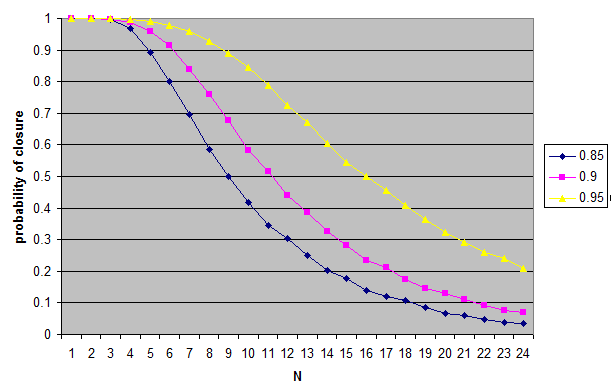
Then there is a simple formula for the probability that the conjunction of randomly chosen distinct Es satisfy the credential threshold condition: (p₀log p₀ + (1 − p₀))/(1 − p₀)². (Fix one credence between p₀ and 1, and calculate the probability that the other credence satisfies the condition; then integrate from p₀ and 1 and divide by 1 − p₀.) We can plug some numbers in.

• At threshold 0.5, probability of conjunction above threshold: 0.61

• At threshold 0.75, probability of conjunction above threshold: 0.55

• At threshold 0.9, probability of conjunction above threshold: 0.52

• At threshold 0.95, probability of conjunction above threshold: 0.51

• At threshold 0.99, probability of conjunction above threshold: 0.502

And the limit as threshold approaches 1 is 1/2.

So, it’s more likely than not that the conjunction satisfies the credential threshold, but on the other hand the probability is not high enough that we can say that it’s typically the conjunction satisfies the threshold.

But the model has two limitations which will affect the above.

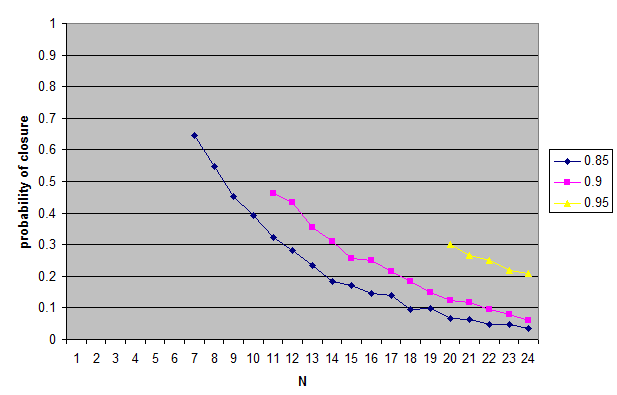
Limitation 1: Intuitively, propositions with positive epistemic or doxastic status are more likely to have a credence closer to the low end of the [t₀, 1] interval, rather than being uniformly distributed over it. This is going to make the probability of the conjunction meeting the threshold be lower than the Simple Model predicts.

Limitation 2: Even without being coherentists, we would expect that our doxastic states to “hang together”. Thus, typically, we would expect that if p and q are propositions that have a credence significantly above 1/2, then typically p and q will have a positive statistical correlation (with respect to credences), so that P(p ∧ q)>P(p)P(q), rather than being independent. This means that the Simple Model underestimates the how often the conjunction is above the threshold. In the extreme case that all our doxastic states are logically equivalent, the conjunction will always meet the threshold condition. In more typical cases, the correlation will be weaker, but we would still expect a significant credential correlation.

So it may well be that even if one takes into account Limitation 1, taking into account Limitation 2 will allow one to say that typically conjunctions of Es meet the threshold condition.

Acknowledgment: I am grateful to John Hawthorne for a discussion of closure and thresholds.

Closure of what is knowable a priori

Plausibly, some true set theoretic axioms can be known a priori with a high degree of confidence. The Axiom of Separation is a good candidate. But other axioms, like the Axiom of Choice or the Continuum Hypothesis, we are much less confident of. Suppose that these axioms are true.

Could smarter beings than we are know them a priori? Maybe, but probably even they would not know them with complete confidence. There will be arguments for the axioms and arguments against the axioms. It seems likely that there will be axioms of set theory that both are true but that no rational being is going to have an a priori degree of confidence greater than, say, 0.99. Moreover, it is likely that there are many such independent axioms, perhaps infinitely many. When you conjoin enough such axioms, the probability of the conjunction will get smaller and smaller for a rational being, until you get to the point where the conjunction will be a priori quite incredible. Thus, there will be conjunctions of a priori knowable axioms that will themselves not be a priori knowable.

Thus the a priori knowable is not closed under conjunction. This does not bother me. As Jon Kvanvig said to me, the a priori is an epistemological category, and so we shouldn't expect closure. But I think this will generate serious problems for anybody like Chalmers who wants to put a heavy philosophical burden on the concept of the a priori.

But maybe someone could have a rational insight into set theory that yields complete certainty as to a controverted axiom, of a sort that remains no matter how many independent axioms are conjoined? For instance, theists are apt to think that God has such an insight. But God is not, I think, an a priori knower of set theory. First, I say that abstract objects are nothing but divine thoughts, and so God knows set theory by introspection, and introspection is more akin to the a posteriori. Second, even apart from such an ontology of sets, it is really hard to see if the rational insight really should count as a priori. I don't know how the rational insight would work, either for God or for a godlike knower, but rational insight into set theory is something like a vision of set theoretic reality. But that's much more like the a posteriori.

Closure for knowledge

Here is a closure principle I don't know a counterexample to:

If you know that that s is the conclusion of a sound argument and (non-aberrantly) therefore believe that s, then you know that s.