This is just a quick technical note. Feel free to ignore. Bas van Fraassen defines a Popper probability measure as a Popper probability function that is defined on a σ-field and such that P(−|B) is a countably additive probability measure for any non-negligible B. We can say that B is negligible provided that P(∅|B)=1. One might hope to define a Popper probability function on, say, [0,1]2 such that if B⊆[0,1]2 is a closed non-self-intersecting smooth curve of non-zero length then B is in our σ-field, is non-negligible and P(−|B) is normalized Lebesgue length measure for Borel subsets of B.
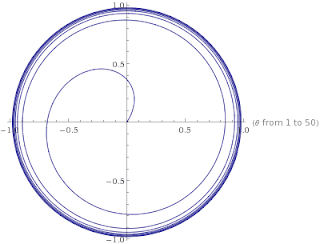
Unfortunately, we can't do this. For consider the infinite-length non-self-intersecting curve B defined in polar coordinates by r=1−1/θ, for θ≥1. This would be non-negligible because finite subcurves of it would be non-negligible. Now chop up B into a sequence of curves of unit length each: B1,B2,.... At least one of these has non-zero probability given B, by countable additivity of P(−|B). But by the Lebesgue length measure condition and Popper function axioms, they must all have the same probability given B. And that will violate additivity of P(−|B).
I suspect that Popper probability measures aren't very interesting: there is too much that ends up negligible, thereby not making much of an improvement over ordinary probability measures.
1 comment:
It's also not hard to prove that an isometrically invariant Popper measure on all Borel subsets of [0,1]^2 makes negligible every line segment.
So, roughly speaking, we am here: Invariant Popper functions on [0,1]^3 make line segments negligible (see comment on an earlier post) while invariant Popper measures on [0,1]^2 make line segments negligible. Wonder how far one could improve on these results (are rectangles negligible for invariant Popper functions on [0,1]^3?).
Post a Comment