Popper probability measure

This is just a quick technical note. Feel free to ignore. Bas van Fraassen defines a Popper probability measure as a Popper probability function that is defined on a σ-field and such that P(−|B) is a countably additive probability measure for any non-negligible B. We can say that B is negligible provided that P(∅|B)=1. One might hope to define a Popper probability function on, say, [0,1]² such that if B⊆[0,1]² is a closed non-self-intersecting smooth curve of non-zero length then B is in our σ-field, is non-negligible and P(−|B) is normalized Lebesgue length measure for Borel subsets of B.

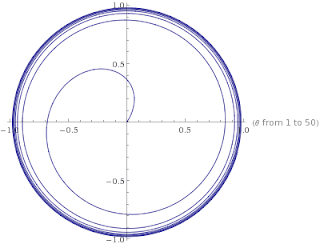
 Unfortunately, we can't do this. For consider the infinite-length non-self-intersecting curve B defined in polar coordinates by r=1−1/θ, for θ≥1. This would be non-negligible because finite subcurves of it would be non-negligible. Now chop up B into a sequence of curves of unit length each: B₁,B₂,.... At least one of these has non-zero probability given B, by countable additivity of P(−|B). But by the Lebesgue length measure condition and Popper function axioms, they must all have the same probability given B. And that will violate additivity of P(−|B).

I suspect that Popper probability measures aren't very interesting: there is too much that ends up negligible, thereby not making much of an improvement over ordinary probability measures.