In an earlier post, I speculated about thresholds and closure without doing any calculations. Now it’s time to do some calculations.
The Question: If you have two propositions that meet a credential threshold, how likely is it that their conjunction does as well? I.e., how likely is closure to hold for pairs of propositions meeting the threshold?
Model 1: Take a probability space with N points. Assign a credence to each of the N points by uniformly choosing a random number in some fixed range, and then normalizing so total probability is 1. Now among the 2N (up to equivalence) propositions about points in the probability space, choose two at random subject to the constraint that they both meet the threshold condition. Check if their conjunction meets the threshold condition. Repeat. The source code is here (MIT license).
The Results: With thresholds ranging from 0.85 to 0.95, as N increases, the probability of the conjunction meeting the threshold goes down. At N = 16, for all three thresholds, it is below 0.5. At N = 24, for all three thresholds, it is below 0.21. In other words, for randomly chosen propositions, we can expect closure to be atypical.
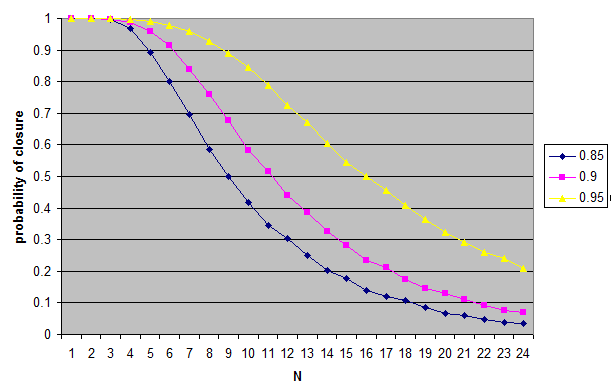
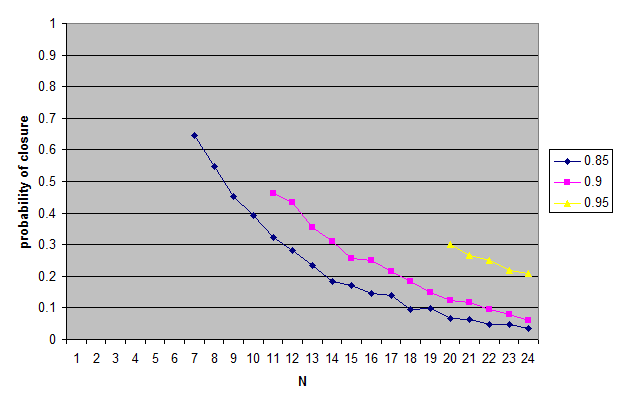
Note: The original model allows the two random propositions to turn out to be the same one. Otherwise, for N such that 1/N < t0, where t0 is the threshold, the probability of closure could be undefined as it might be impossible to generate two distinct propositions that meet the closure condition. Dropping the condition that allows the two random propositions to be the same will only make the probability of closure smaller. Here (also MIT license) is the modified code that does this. The results are here.
Final Remarks: This suggests that if the justification condition for knowledge is expressed in terms of a credence threshold, closure for knowledge will be atypical: i.e., for a random pair of propositions one knows, it will be unlikely that one will know the conjunction. Of course, it could be that the other conditions for knowledge, besides justification, will affect this, by making closure somewhat more likely. But I don’t have reason to think it will make an enormous difference. So, if one thinks closure should be typical, one shouldn’t think that justification is described by a credence threshold.
I go the other way: I think justification is described by a credence threshold, and now I think that closure is unlikely to be typical.
A limitation in the above models is that the propositions we normally talk about are not randomly chosen from the 2N propositions describing the probability space.
1 comment:
One of my half-baked views is that we only make our mental representations as complicated as they need to be. So for most beliefs, we have a binary true/false model. These would be closed under conjunction. But when we work harder, we assign things like credences (typically rough and vague ones, and getting more sophisticated as necessary. For yet more sophisticated beliefs, we might add a probability distribution.) For these, closure would fail for reasons you point out. It is a terminological issue whether we want to call all of these things "beliefs" but it's good to see what the tradeoffs here are.
Post a Comment